Big O Notation Basics for Web Developers

As a web developers, we strive to not just write code that works, but also code that is efficient. That’s where Big O Notation comes in. It is a concept from computer science that helps us describe how the performance of an algorithm changes as the size of the input grows. For example, when you are looping through an array or building a full-stack app, Big O can help you write smarter, faster code.

What Is Big O Notation?

Big O notation is a mathematical concept used in computer science to describe the performance of an algorithm. Specifically, it measures how the run-time or space requirements of an algorithm grow as the input size increases. For example Big O notation helps you predict things like if a function will still run quickly if it has a million users?

Understanding Big O can help you choose better algorithms and avoid slow, bloated apps.

What is a Quadratic Function (O(n^2))

A quadratic function describes an algorithm whose performance is proportional to the square of the input size. This is typically seen in algorithms with nested loops, where for every element, you loop over the entire dataset again.

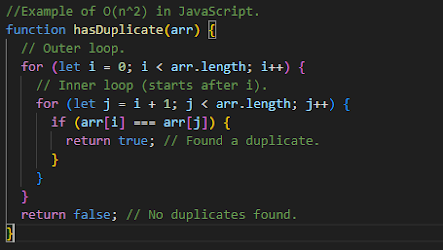
Example of O(n^2) in JavaScript:

What is happening here?

1. The outer loop runs n times.
2. For each iteration of the outer loop, the inner loop runs up to n times.
3. So the total number of operations is roughly n * n, or n^2.

What it does:
This function checks if there are any duplicate values in the array.

Why O(n²)?
There are two nested loops, and the inner loop compares each element with every other element after it. For large arrays, this results in a huge number of comparisons:

• 10 elements > 45 comparisons
• 100 elements > 4,950 comparisons

Comparing Linear Search vs Binary Search

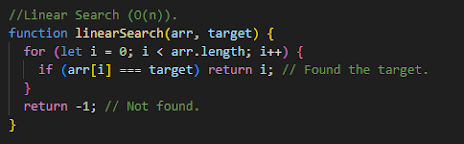
Linear Search (O(n))

A Linear Search, searches each item in the list one by one.

What it does:
Goes through the array one item at a time to find the target value.

Why O(n)?
In the worst case, it checks every element once. If there are n items, it takes n steps.

Describe in Big O: O(n) > worst case is that it checks every element.

Binary Search (O(log n))

Requires the list to be sorted. It divides the search space in half each time.

What it does:
Searches a sorted array by splitting it in half each time.

Why O(log n)?
Each time, it cuts the search space in half:

• 1000 items > at most 10 checks
• 1,000,000 items > at most 20 checks

Describe in Big O: O(log n) > the input is halved with every step, making it much faster.

Which is More Efficient?

Binary search is far more efficient for large datasets, but only works on sorted data.

What is the Fibonacci Sequence

The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones.

Fibonacci numbers: 1, 1, 2, 3, 5, 8, 13, 21...

Recursive Fibonacci (O(2^n))

What it does:
Calculates the nth Fibonacci number recursively.

Why O(2ⁿ)?
Each call makes 2 more calls, and those calls each make 2 more, and so on. This grows very fast.

• fibonacci(5) = 15 calls
• fibonacci(10) = 177 calls
• fibonacci(20) = 21,891 calls

Big O: O(2^n)

This is very inefficient for large numbers. It repeats calculations, leading to exponential growth.

Iterative Fibonacci (O(n))

What it does:
Generates the first n numbers of the Fibonacci sequence using a loop.

Why O(n)?
It calculates each number only once and stores it in the array, no repetition, no recursion.

Big O: O(n)

Much faster and more efficient than the recursive version.

Which is More Efficient?

Both give the same result, but the iterative method is far more efficient. It's faster, easier to read, and scales well with larger numbers.